The theory of ultra-cold atomic gases

Researchers at the Dodd-Walls Centre for Photonic and Quantum Technologies, including Dr Danny Baillie of the Department of Physics, University of Otago, have used NeSI’s resources to help analyse the use of ultra-cold atomic gases.

Gases have recently been cooled to a billionth of a degree above absolute zero, at which point everyday thermal noise is almost totally absent and the quantum mechanical behaviour of the particles is revealed. Magnetic fields and lasers are used to confine and manipulate the gas, and even control how the atoms or molecules interact with each other. The properties of the gas can be measured in real time, typically with optical imaging, which can be used to measure the gas density on micrometre length scales. These systems are of interest in physics for fundamental studies of quantum physics and for applications into next-generation atomic clocks and quantum computers.

A feature of these ultra-cold gases is that the interactions between the particles are extremely well characterised, offering the opportunity for first-principles calculations to compare with experiment. A recent development in the field has been the production of cold samples of dipolar particles, in which the interactions between the particles is like that between two bar magnets: both long-ranged and dependent on the orientation of the particles. This interaction leads to new physical phenomena that can be explored in these systems, however the partially attractive character of the interaction (e.g. two bar magnets placed head to tail attract each other) also means the gas can be unstable and collapse, meaning the gas is lost to the experiment. When a collapse occurs it involves a complex interplay of the geometry of the confined gas, the temperature of the system, and the precise properties of the interactions. This work establishes a comprehensive theory for the conditions where the gas is stable, which is vital to providing a map for experimentalists for how to prepare and manipulate these systems.

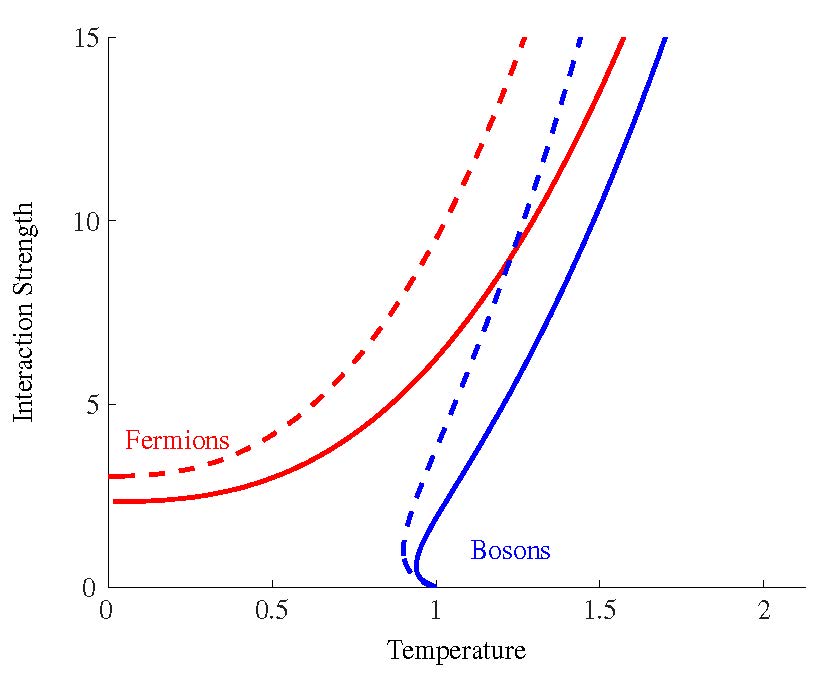
According to quantum mechanics, particles of the same species are fundamentally indistinguishable: if two of them were exchanged it would be impossible to tell. Particles come in two flavours depending on the number of constituent electrons, protons and neutrons: an odd number and they are fermions; an even number and they are bosons. For fermions, the effect of exchange gives rise to the Pauli exclusion principle: two of them cannot occupy the same quantum state. The coldest bosons occupy the lowest energy state, a Bose Einstein Condensate. The exchange effect means that cold fermions are significantly more stable than bosons. Fully allowing for the exchange effect is computationally difficult: it is necessary to model both the density of the particles and their relative position. Even exploiting the cylindrical symmetry of the problem, the system has four effective dimensions and interaction effects need to be solved self-consistently. 

Due to this difficulty, the researchers’ earlier work[1] was not able to fully allow for the exchange effect, but this was rectified by using their newly developed algorithm[2] with the computational power provided by NeSI’s Pan Cluster.

Dr Baillie says, “By using NeSI's resources we were also able to evaluate the stability at our full range of temperatures in parallel, simultaneously using almost a thousand cores, which enabled us to complete the work in a fraction of the time it would've taken using only local resources.”

Fig.1 shows that the exchange effect is significant.

Attribution: 

Fig.1 Relationship between interaction strength and temperature at the instability point for a pancake geometry: fully allowing for exchange (solid) makes the gas less stable than earlier work (dashed). Note that fermions (red) are more stable than bosons (blue).